| Feed-forward reflection rendering |
| The sample-based camera (SBC) is a general camera constructed from a given set of rays. The first application of SBCs that we have explored is rendering accurate reflections on curved reflectors at interactive rates. In order to render reflections with the feed forward graphics pipeline, one has to compute the image points where a reflected scene point projects. For general reflectors, the problem of projecting reflected vertices does not have a closed form solution. The SBC is a collection of BSP trees of pinhole cameras that jointly approximate the projection function. One BSP tree is built for each convex component of the reflector. The projection error is controlled by the user, the typical upper bound we use is 1 pixel. The method supports change of view, moving objects and reflectors, higher order reflections, view-dependent lighting of reflected objects, and complex reflector surface properties. The SBC approach excels in the case of large smooth reflectors like the ones in the images below. Complex reflectors perturb the desired image rays considerably: less coherence and more intersections make the hierarchical space partitioning less efficient. We handle complex reflectors with a different approach, based on approximating the reflected scene with impostors. |
  
Environment mapping, SBC (60fps), and ray tracing. |
 
Fresnel & attenuation with distance effects. |
 
1st and 2nd order reflections rendered with SBC (left, 30 fps) and ray tracing (right). Image resolution: 1140×960. |
| The class of k-ray cameras |
| The SBC provides an efficient and accurate approximation of a set of rays by leveraging ray coherence. The initial set of rays is subdivided recursively in bundles until a bundle can be approximated well enough with a simple camera. A simple camera is a camera with closed form projection. In the first implementation of SBCs simple cameras were modeled as planar pinhole cameras. Next we looked at devising models for the simple cameras that are more powerful, in the sense of providing a better approximation for a given set of rays. For this we developed the class of k-ray non-pinhole cameras. A k-ray camera is built from k given rays and has closed form projection. We have shown that such cameras exist for k up to 6, when the projection equation has order 4. A versatile simple camera model is the continuous 3-ray camera (C3RC), since it offers projection continuity across the edge shared by two adjacent cameras. |
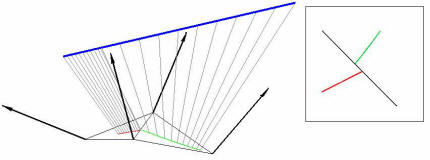 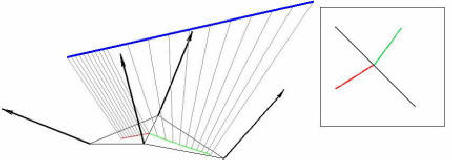
Continuity problem across shared edge eliminated by continuous 3-ray cameras (C3RCs). |
 
Images rendered with two adjacent regular 3-ray cameras and C3RCs, respectively. |

|

