| Summary |
The quality of an appearance edit is directly related to the resolution achievable by the projectors available. Various factors affect a projector's resolution and radiant power, including the projector's distance to the object and the orientation of the projector to the object. In this work, we analyze the appearance editing setup and projector pixel interaction to improve the quality of our appearance edits. Our projectors are set up such that their fields of projection are superimposed on the object's surface, and we model projector pixels as elliptical Gaussians. Thus, we require inverting a complex multi-projector light transport matrix via a constrained optimization when modeling the projector pixel interaction. We also introduce a technique to swap quickly between different appearances without having to recalculate full compensation images.
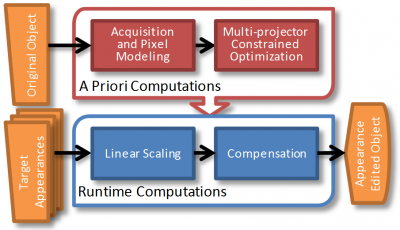
Below is a figure of our appearance editing pipeline. Using the original object as input, acquiring a 3D model of the object, calibrating the projectors and camera, projector pixel modeling, and inverting the multi-rojector light transport matrix are performed once per object as a priori computations. Then, at runtime, any target appearance can be applied quickly to produce our appearance edited objects. |
 |
| As shown in the below figures, our technique is capable of performing a wide variety of appearance edits (e.g., producing a subsurface scattering appearance or a glossy appearance with inter-reflections) at higher resolutions than possible with prior approaches. |
 |
| a) The original object, and b) has leaves added onto the vase. c-e) contain various appearances imparted on the object shown in the inset. Swapping between these appearances only takes a second. f-g) Two appearances of a colored Beethoven at different points in a nodding animation (original object in inset). |
 |
| Improved Resolution |
| When appearance editing with arbitrarily shaped objects, it is inevitable that a single projector will illuminate a portion of the object's surface at a grazing angle. This symptom yields a poor appearance edit at the problematic area. In contrast, our setup uses multiple superimposing projections. We observe that this reduces the probability that any surface area is being illuminated at only grazing angles (i.e., in all likelihood at least one projector is reasonably illuminating each surface point being edited). Thus, the resolution achieved at grazing angles is improved. In the below figure, we demonstrate this issue by imparting a checkerboard pattern onto a pedestal object in a). b) shows the resulting appearance when only a single projector is used; significant aliasing is present. c) shows the result using our system which displays improved appearance resolution. |
 |
| Further, superimposed projections enables areas which are being illuminated head-on by multiple projectors to achieve improved resolution. This is done by modeling the interaction between multiple overlapping projector pixels from multiple projectors. In the figure below, we compare the appearances achieved using previous works against our result in a zoom-in of an appearance shown in the summary. a) shows the appearance achieved with a naive solution of inverting the multi-projector light transport matrix. b) shows the appearance achieved when a) is improved by constraining the pixel intensity values between [0, 1] when inverting the multi-projector light transport matrix. c) shows the appearance achieved using our system which includes adding smoothness constraints, regularizing the positions of the projector pixels on the object, and modeling each projector pixel as an elliptical Gaussian. |
 |
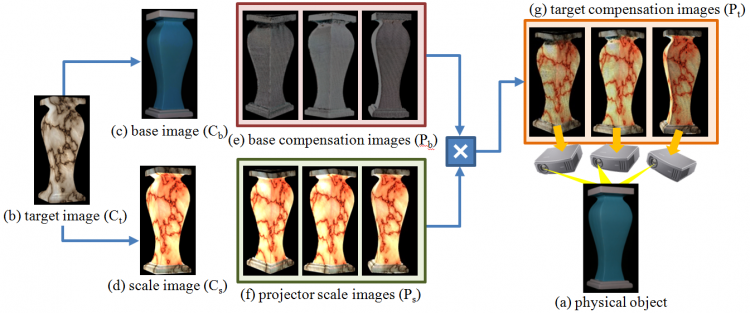
| Base-Scale Decomposition |
| We achieve the ability to quickly swap between multiple target appearances by decomposing each target appearance into a base image and a scale image. This decomposition enables the multi-projector light transport matrix to be solved only once per object (as opposed to once per target appearance). Then, for a given target appearance at runtime, compensation images are computed by a per-pixel multiplication of the base image (common for an object) by the scale image (common for a target appearance). |
 |
| Technical Aspects |
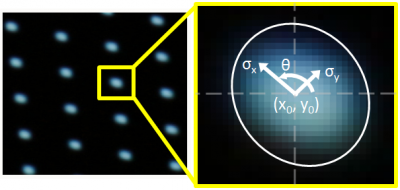
| Throughout our system, we use a variety of algorithms to help improve the quality of our appearance edits. We model projector pixels projected on the object's surface as elliptical Gaussians we call metapixels. We find this representation of a projector pixel projected on the object's surface to be more accurate than a point or quadrilateral. |
 |
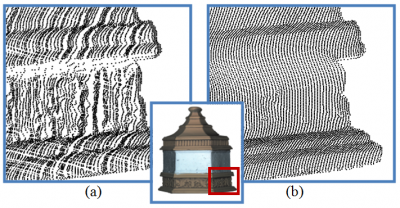
| Prior to solving the constrained optimization, we also regularize the positions of the metapixels in order to avoid striations and other visual artifacts in the final appearance. An example of regularization is shown below, with the un-regularized metapixel locations shown in a) and the regularized metapixel locations shown in b). |
 |
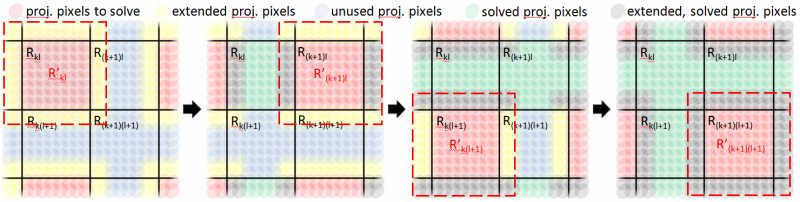
| In order to solve the constrained optimization efficiently, we use a parallel solving algorithm (shown below) which divides the (camera space) base image into four groups of regions R, each group to be solved in parallel. With each successive group being solved, additional constraints are added from the previous groups to ensure continuity and a smooth appearance. We also add smoothness constraints to the constrained optimization in order to achieve smoother appearances. |
 |

|

